Bài toán cực trị của mạch RLC mắc nối tiếp
Bài làm:
CỰC TRỊ CỦA DÒNG ĐIỆN XOAY CHIỀU
I. R thay đổi
1. R THAY ĐỔI ĐỂ PMAX
a. Mạch RLC có cuộn dây thuần cảm (r=0)
\(P = UIc{\rm{os}}\varphi {\rm{ = }}{{\rm{I}}^2}R = \frac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \frac{{{U^2}}}{{R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)
Để \({P_{max}} \to {\left( {R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right)_{\min }}\)
Ta có: \(R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R\frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} = 2\left| {{Z_L} - {Z_C}} \right|\)
Dấu “=” xảy ra \( \leftrightarrow {R^2} = {({Z_L} - {Z_C})^2} \to R = \left| {{Z_L} - {Z_C}} \right|\)
b. Mạch RLC có cuộn dây không thuần cảm (r≠0)
- Công suất trên toàn mạch:
\(P{\rm{ = }}{{\rm{I}}^2}(R + r) = \frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}(R + r) = \frac{{{U^2}}}{{R + r + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}}}\)
Để \({P_{max}} \to {\left( {R + r + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}} \right)_{\min }}\)
Ta có: \((R + r) + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}} \ge 2\sqrt {(R + r)\frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}} = 2\left| {{Z_L} - {Z_C}} \right|\)
Dấu “=” xảy ra \( \leftrightarrow {(R + r)^2} = {({Z_L} - {Z_C})^2} \to R + r = \left| {{Z_L} - {Z_C}} \right| \to R = \left| {{Z_L} - {Z_C}} \right| - r\)
Chú ý: Nếu \(r > {Z_L} - {Z_C} \to {P_{{\rm{max}}}} \leftrightarrow R = 0,{P_{{\rm{max}}}} = \frac{{{U^2}}}{{{r^2} + {{({Z_L} - {Z_C})}^2}}}r\)
- Công suất trên R: \(P{\rm{ = }}\frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \frac{{{U^2}}}{{R + 2r + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)
\(\begin{array}{l}A = R + 2r + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}\\{A_{\min }} \leftrightarrow {\left( {R + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right)_{\min }}\\R + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R.\frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} = 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array}\)
Dấu “=” xảy ra: \( \leftrightarrow {R^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2},{P_{{\rm{max}}}} = \frac{{{U^2}}}{{2{\rm{r}} + 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
- Công suất trên r: \({P_r}{\rm{ = }}\frac{{{U^2}r}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
\({P_{r{\rm{ }}max}} = \frac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\) xảy ra khi R=0
2. KHI R=R1 HOẶC R=R2 THÌ P CÓ CÙNG 1 GIÁ TRỊ (P<PMAX) (CUỘN DÂY THUẦN CẢM)
\(\begin{array}{l}P = \frac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R\\ \to P({R^2} + {\left( {{Z_L} - {Z_C}} \right)^2}) = {U^2}R\\ \leftrightarrow P{R^2} - {U^2}R + {\left( {{Z_L} - {Z_C}} \right)^2}P = 0\\ \leftrightarrow {R^2} - \frac{{{U^2}R}}{P} + {\left( {{Z_L} - {Z_C}} \right)^2} = 0{\rm{ }}(1)\end{array}\)
PT (1) có 2 nghiệm: R1, R2 : \(\left\{ \begin{array}{l}{R_1} + {R_2} = \frac{{{U^2}}}{P}\\{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} \end{array} \right.\)
II. C thay đổi
1. C THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG \({\varphi _{{\bf{U}}/{\bf{I}}}} = {\bf{0}}\) VÀ \({{\bf{I}}_{{\bf{MAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{RMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LCMIN}}}}\)
\({Z_L} = {Z_C}\)
Khi đó:
\(\begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0
2. C THAY ĐỔI ĐỂ UCMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URL
Ta có: \({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Chia cả tử và mẫu cho ZL, ta được: \({U_C} = \dfrac{U}{{\sqrt {\dfrac{{{R^2}}}{{{Z_C}^2}} + \frac{{{{({Z_L} - {Z_C})}^2}}}{{{Z_C}^2}}} }} = \dfrac{U}{{\sqrt {\dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1} }}\)
Đặt \(y = \dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1 = ({R^2} + Z_L^2){x^2} - 2{Z_L}x + 1\) với $x = \dfrac{1}{{{Z_C}}}$
Ta có UCmax khi ymin
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2{Z_L}}}{{2({R^2} + Z_L^2)}} \to {Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
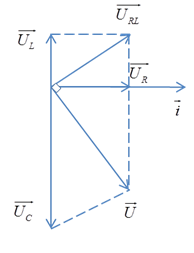
Khi đó: \({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)
Hệ quả: \(\left\{ \begin{array}{l}{U_{RL}} \bot {U_{AB}}\\U_{C\max }^2 = {U^2} + U_{RL}^2 = {U^2} + U_R^2 + U_L^2\\U_{C\max }^{}.{U_R} = U.{U_{RL}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\end{array} \right.\)
3. C THAY ĐỔI ĐỂ URCMAX
Ta có: \({U_{RC}} = I{Z_{RC}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} }}\)
\({U_{RLmax}} \leftrightarrow {\left( {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} \right)_{\min }}\)
\(\begin{array}{*{20}{l}}{y = 1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}}\\{y' = {{(1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}})}^\prime } = \dfrac{{2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_C^2)}^2}}}}\\{y' = 0 \leftrightarrow 2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C} = 0}\\{\left\{ \begin{array}{l}{Z_C} > 0\\{Z_C} = \dfrac{{ - b + \sqrt \Delta }}{{2a}} = \dfrac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2}\end{array} \right.}\end{array}\)
Khi đó:
\({{U}_{RC\max }}=\frac{2UR}{\sqrt{4{{R}^{2}}+Z_{L}^{2}}-{{Z}_{L}}}\)
4. C THAY ĐỔI ĐỂ URL KHÔNG PHỤ THUỘC VÀO R
URL không phụ thuộc vào R
\( \leftrightarrow {U_{RL}} = {U_{AB}}\)
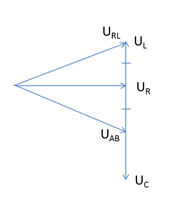
Từ giản đồ:
\(\begin{array}{l} \to {U_C} = 2{U_L}\\ \to {Z_C} = 2{Z_L}\end{array}\)
5. C THAY ĐỔI ĐỂ \({U_{RC}} \bot {U_{RL}}\)
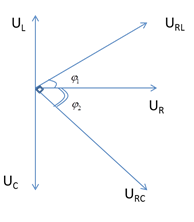
\(\begin{array}{l}{U_{RL}} \bot {U_{RC}}\\ \leftrightarrow \left\{ \begin{array}{l}\sin {\varphi _1} = c{\rm{os}}{\varphi _2}\\c{\rm{os}}{\varphi _1} = \left| {\sin {\varphi _2}} \right|\end{array} \right. \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\\ \leftrightarrow \frac{{{U_L}}}{{{U_R}}}\frac{{{U_C}}}{{{U_R}}} = 1 \leftrightarrow {U_L}{U_C} = {U_R}^2 \leftrightarrow {Z_L}{Z_C} = {R^2}\end{array}\)
6. C=C1 HOẶC C=C2 THÌ UC CÓ CÙNG GIÁ TRỊ
\({C_1} + {C_2} = 2{C_{max}} = 2{C_0} \to {C_0} = \dfrac{{{C_1} + {C_2}}}{2}\)
7. C THAY ĐỔI CÓ 2 GIÁ TRỊ LÀM CHO: \({{\bf{I}}_{\bf{1}}} = {{\bf{I}}_{\bf{2}}},{\rm{ }}{{\bf{P}}_{\bf{1}}} = {{\bf{P}}_{\bf{2}}},{\rm{ }}{\bf{cos}}{\varphi _{\bf{1}}} = {\bf{cos}}{\varphi _{\bf{2}}},{\rm{ }}{{\bf{Z}}_{\bf{1}}} = {{\bf{Z}}_{\bf{2}}}\)
- Z1=Z2
\({R^2} + {({Z_L} - {Z_{C1}})^2} = {R^2} + {({Z_L} - {Z_{C2}})^2} \to \left| {{Z_L} - {Z_{C1}}} \right| = \left| {{Z_L} - {Z_{C2}}} \right|\)
Với ZC2>ZC1 \( \to {Z_{C1}} + {Z_{C2}} = 2{Z_L}\)
- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện
\( \leftrightarrow \left\{ \begin{array}{l}I = {I_{{\rm{max}}}}\\{\varphi _u} = {\varphi _i}\\\left| {{\rm{cos}}\varphi } \right| = 1\end{array} \right. \to 2{Z_{Cm{\rm{ax}}}} = {Z_{C1}} + {Z_{C2}}\)
III. L thay đổi
1- L THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG \({\varphi _{{\bf{u}}/{\bf{i}}}} = {\bf{0}}\) VÀ IMAX, URMAX, UCMAX, ULCMIN
\({Z_L} = {Z_C}\)
Khi đó:
\({Z_{\min }} = R,{\rm{ }}{I_{{\rm{max}}}} = \frac{U}{R},{\rm{ }}{P_{{\rm{max}}}} = {I^2}R = \frac{{{U^2}}}{R}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0I
2 - L THAY ĐỔI ĐỂ ULMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URC
Ta có: \({U_L} = I{Z_L} = \frac{{U{Z_L}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Chia cả tử và mẫu cho ZL, ta được: \({U_L} = \frac{U}{{\sqrt {\frac{{{R^2}}}{{{Z_L}^2}} + \frac{{{{({Z_L} - {Z_C})}^2}}}{{{Z_L}^2}}} }} = \frac{U}{{\sqrt {\frac{{{R^2} + Z_C^2}}{{{Z_L}^2}} - \frac{{2{Z_C}}}{{{Z_L}}} + 1} }}\)
Đặt \(y = \frac{{{R^2} + Z_C^2}}{{{Z_L}^2}} - \frac{{2{Z_C}}}{{{Z_L}}} + 1 = ({R^2} + Z_C^2){x^2} - 2{Z_C}x + 1\) với $x = \frac{1}{{{Z_L}}}$
Ta có ULmax khi ymin
\({y_{\min }} \leftrightarrow x = - \frac{b}{{2{\rm{a}}}} = \frac{{2{Z_C}}}{{2({R^2} + Z_C^2)}} \to {Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)
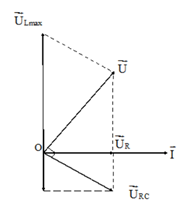
Khi đó: \({U_{Lm{\rm{ax}}}} = \frac{{U_R^2 + U_C^2}}{{{U_C}}} = \frac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)
Hệ quả: \(\left\{ \begin{array}{l}{U_{RC}} \bot {U_{AB}}\\U_{L\max }^2 = {U^2} + U_{RC}^2 = {U^2} + U_R^2 + U_C^2\\U_{L\max }^{}.{U_R} = U.{U_{RC}}\\\frac{1}{{U_R^2}} = \frac{1}{{{U^2}}} + \frac{1}{{U_{RC}^2}}\end{array} \right.\)
3 - L THAY ĐỔI ĐỂ URLMAX
Ta có: \({U_{RL}} = I{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \frac{U}{{\sqrt {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} }}\)
URLmax \( \leftrightarrow {\left( {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} \right)_{\min }}\)
\(\eqalign{& y = 1 + \frac{{ - 2{Z_L}{Z_C} + Z_C^2}}{{{R^2} + Z_L^2}} \cr & y' = \left( {1 + \frac{{ - 2{Z_L}{Z_C} + Z_C^2}}{{{R^2} + Z_L^2}}} \right)' = \frac{{2Z_L^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_L^2)}^2}}} \cr & y' = 0 \leftrightarrow 2Z_L^2 - 2{R^2} - 2{Z_L}{Z_C} = 0 \cr} \)
\({Z_L} > 0,{Z_L} = \frac{{ - b + \sqrt \Delta }}{{2a}} = \frac{{{Z_C} + \sqrt {4{R^2} + Z_C^2} }}{2}\)
Khi đó:
\({U_{R{L_{\max }}}} = \frac{{2UR}}{{\sqrt {4{R^2} + Z_C^2} - {Z_C}}}\)
4 - L THAY ĐỔI ĐỂ URC KHÔNG PHỤ THUỘC VÀO R
URC không phụ thuộc vào R
\( \leftrightarrow {U_{RC}} = {U_{AB}}\)
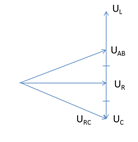
Từ giản đồ:
\(\begin{array}{l} \leftrightarrow {U_C} = {U_L} - {U_C}\\ \to {U_L} = 2{U_C}\\ \to {Z_L} = 2{Z_C}\end{array}\)
5 - L THAY ĐỔI ĐỂ \({U_{RC}} \bot {U_{RL}}\)
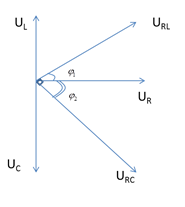
\(\begin{array}{l}{U_{RL}} \bot {U_{RC}}\\ \leftrightarrow \left\{ \begin{array}{l}\sin {\varphi _1} = c{\rm{os}}{\varphi _2}\\c{\rm{os}}{\varphi _1} = \left| {\sin {\varphi _2}} \right|\end{array} \right. \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\\ \leftrightarrow \frac{{{U_L}}}{{{U_R}}}\frac{{{U_C}}}{{{U_R}}} = 1 \leftrightarrow {U_L}{U_C} = {U_R}^2 \leftrightarrow {Z_L}{Z_C} = {R^2}\end{array}\)
6 - L=L1HOẶC L=L2 THÌ UL CÓ CÙNG GIÁ TRỊ
\(\frac{1}{{{L_{{\rm{max}}}}}} = \frac{1}{2}(\frac{1}{{{L_1}}} + \frac{1}{{{L_2}}})\)
7 - L THAY ĐỔI, CÓ 2 GIÁ TRỊ CỦA L LÀM CHO \({{\bf{I}}_{\bf{1}}} = {{\bf{I}}_{\bf{2}}},{\rm{ }}{{\bf{P}}_{\bf{1}}} = {{\bf{P}}_{\bf{2}}},{\rm{ }}{\bf{cos}}{\varphi _{\bf{1}}} = {\bf{cos}}{\varphi _{\bf{2}}},{\rm{ }}{{\bf{Z}}_{\bf{1}}} = {{\bf{Z}}_{\bf{2}}}\)
- Z1=Z2
\({R^2} + {({Z_{L1}} - {Z_C})^2} = {R^2} + {({Z_{L2}} - {Z_C})^2} \to \left| {{Z_{L1}} - {Z_C}} \right| = \left| {{Z_{L2}} - {Z_C}} \right|\)
Với ZL2>ZL1 \( \to {Z_{L1}} + {Z_{L2}} = 2{Z_C}\)
- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện
\( \leftrightarrow \left\{ \begin{array}{l}I = {I_{{\rm{max}}}}\\{\varphi _u} = {\varphi _i}\\\left| {{\rm{cos}}\varphi } \right| = 1\end{array} \right. \to L = \frac{{{L_1} + {L_2}}}{2}\)
IV. \(\omega\) thay đổi
1. \(\omega \) THAY ĐỔI ĐỂ XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG ĐIỆN: \({Z_{min}},{\rm{ }}{I_{max}},{\rm{ }}{U_{Rmax}},{\rm{ }}{P_{ABmax}},{\rm{ }}cos\varphi \) CỰC ĐẠI
\({Z_L} = {Z_C} \to {\omega ^2} = \frac{1}{{LC}}{\rm{ hay }}\omega = \frac{1}{{\sqrt {LC} }}\)
Khi đó:
\({Z_{\min }} = R,{\rm{ }}{I_{{\rm{max}}}} = \dfrac{U}{R},{\rm{ }}{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: \(\varphi = 0\)
2. \(\omega \) THAY ĐỔI ĐỂ UCMAX
\({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\omega C\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{U}{{C\sqrt {{\omega ^4}{L^2} + ({R^2} - 2\dfrac{L}{C}){\omega ^2} + \dfrac{1}{{{C^2}}}} }}\)
UC max <=> mẫu min
Đặt \({\omega ^2} = x\) , \( \to {x^2}{L^2} + ({R^2} - 2\dfrac{L}{C})x + \dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{{R^2}}}{{LC}} - \dfrac{{{R^4}}}{{2{L^2}}}\)
Khi đó ta có:
\(\begin{array}{l}{Z_L} = \omega L = \sqrt {\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}} L \to Z_L^2 = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_L^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \to \dfrac{{{R^2}}}{2} = {Z_L}\left( {{Z_C} - {Z_L}} \right)\\ \to \dfrac{{{Z_L}}}{R}\dfrac{{\left( {{Z_C} - {Z_L}} \right)}}{R} = \dfrac{1}{2} \leftrightarrow \tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
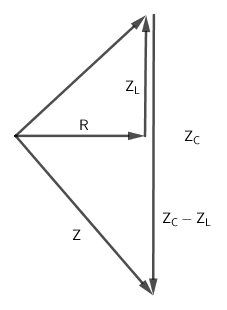
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_C} - {Z_L}} \right)^2} = 2{Z_L}\left( {{Z_C} - {Z_L}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_C^2 - Z_L^2\end{array}\)
Kết luận: \(\omega \) biên thiên để \({U_{{C_{max}}}}\), khi đó:
\({U_{Cm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}\)
\(\tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\) và \(Z_C^2 = {Z^2} + Z_L^2\)
3. \(\omega \) THAY ĐỔI ĐỂ ULMAX
\({U_L} = I{Z_L} = \dfrac{{U{Z_L}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\omega L}}{{\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{{UL}}{{\sqrt {{L^2} + \dfrac{{({R^2} - 2\dfrac{L}{C})}}{{{\omega ^2}}} + \dfrac{1}{{{\omega ^4}{C^2}}}} }}\)
\({U_{L{\rm{ }}max}}\) <=> mẫu min
Đặt \(\dfrac{1}{{{\omega ^2}}} = x\), \( \to {L^2} + ({R^2} - 2\dfrac{L}{C})x + {x^2}\dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2LC - {R^2}{C^2}}}{2},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{4L{{\rm{R}}^2} - {R^4}C}}{4}C\)
Khi đó ta có:
\(\begin{array}{l} \to Z_C^2 = \dfrac{1}{{{\omega ^2}{C^2}}} = \dfrac{1}{{\dfrac{2}{{2LC - {R^2}{C^2}}}{C^2}}} = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_C^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow \dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right) \leftrightarrow \dfrac{{{Z_C}}}{R}\dfrac{{\left( {{Z_L} - {Z_C}} \right)}}{R} = \dfrac{1}{2}\\ \leftrightarrow \tan {\varphi _{RC}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
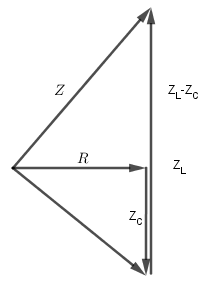
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = 2{Z_C}\left( {{Z_L} - {Z_C}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_L^2 - Z_C^2\end{array}\)
Kết luận: \({U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{2}{{2LC - {R^2}{C^2}}}\)
\(\tan {\varphi _{RC}}\tan \varphi =- \dfrac{1}{2}\) và \(Z_L^2 = {Z^2} + Z_C^2\)
Khi \(\omega \) thay đổi để \({U_{Cmax}},{\rm{ }}{U_{Lmax}}\)
\(\begin{array}{l}{U_{Cm{\rm{ax}}}} = {U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }}\\{\omega _L}.{\omega _C} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
4. THAY ĐỔI \(f\) CÓ HAI GIÁ TRỊ \({f_{\bf{1}}} \ne {f_{\bf{2}}}\) BIẾT \({f_{\bf{1}}} + {f_{\bf{2}}} = {\rm{ }}{\bf{a}}\) VÀ CÙNG CÔNG SUẤT HOẶC CÙNG \({\bf{I}},{\bf{Z}},{\bf{cos}}\varphi ,{{\bf{U}}_{{\bf{R}}.}}\)
- Hai giá trị tần số làm cho mạch có cùng công suất nên:
\(\begin{array}{l}{P_1} = {P_2} \Leftrightarrow I_1^2R = I_2^2R \Leftrightarrow I_1^2 = I_2^2\\ \to \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\ \to {({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2} \to \left[ \begin{array}{l}{Z_{L1}} - {Z_{C1}} = {Z_{L2}} - {Z_{C2}}(loai)\\{Z_{L1}} - {Z_{C1}} = - ({Z_{L2}} - {Z_{C2}})\end{array} \right.\\ \to {Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{C2}}) \to L({\omega _1} + {\omega _2}) = \dfrac{1}{C}(\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}) = \dfrac{1}{C}\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
- Công thức trên áp dụng cho bài toán thay đổi f có cùng I, Z, cosφ, UR
Các hệ quả thu được:
- Cảm kháng và dung kháng trong hai trường hợp:
\({({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2}{\rm{ hay }}\left| {{Z_L} - {Z_C}} \right| = h/s \to \left| \begin{array}{l}{Z_{L1}} = {Z_{C2}}\\{Z_{L2}} = {Z_{C1}}\end{array} \right.\)
- Hệ số công suất trong hai trường hợp: \({\rm{cos}}{\varphi _1} = {\rm{cos}}{\varphi _2} = \dfrac{1}{{\sqrt {1 + k{{(\sqrt {\dfrac{{{\omega _1}}}{{{\omega _2}}}} - \sqrt {\dfrac{{{\omega _2}}}{{{\omega _1}}}} )}^2}} }}{\rm{ (}}\dfrac{L}{C} = k.{R^2})\)
- Cường độ dòng điện trong hai trường hợp: \({I_1} = {I_2} = \dfrac{{{I_{{\rm{max}}}}}}{n}\)
Điện trở của mạch được xác định: \(R = L\dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{\sqrt {{n^2} - 1} }} = \dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{{\omega _1}{\omega _2}C\sqrt {{n^2} - 1} }}\)
Xem thêm Bài tập & Lời giải
Trong bài: Bài 14. Mạch có R, L, C mắc nối tiếp
Bài tập & Lời giải:
- 👉 Câu C1 trang 75 SGK Vật lý 12
- 👉 Câu C2 trang 76 SGK Vật lý 12
- 👉 Câu C3 trang 77 SGK Vật lý 12
- 👉 Bài 1 trang 79 SGK Vật lí 12
- 👉 Bài 2 trang 79 SGK Vật lí 12
- 👉 Bài 3 trang 79 SGK Vật lí 12
- 👉 Bài 4 trang 79 SGK Vật lí 12
- 👉 Bài 5 trang 79 SGK Vật lí 12
- 👉 Bài 6 trang 79 SGK Vật lí 12
- 👉 Bài 7 trang 80 SGK Vật lí 12
- 👉 Bài 8 trang 80 SGK Vật lí 12
- 👉 Bài 9 trang 80 SGK Vật lí 12
- 👉 Bài 10 trang 80 SGK Vật lí 12
- 👉 Bài 11 trang 80 SGK Vật lí 12
- 👉 Bài 12 trang 80 SGK Vật lí 12
Lý thuyết:
Xem thêm lời giải SGK Vật lí lớp 12
CHƯƠNG I. DAO ĐỘNG CƠ
- 👉 Bài 1. Dao động điều hòa
- 👉 Bài 2. Con lắc lò xo
- 👉 Bài 3. Con lắc đơn
- 👉 Bài 4. Dao động tắt dần dao động cưỡng bức
- 👉 Bài 5. Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ FRE-NEN
- 👉 Bài 6. Thực hành: Khảo sát thực nghiệm các định luật dao động của con lắc
- 👉 Đề kiểm tra 15 phút – Chương 1 – Vật lí 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Vật lí 12
CHƯƠNG II. SÓNG CƠ VÀ SÓNG ÂM
- 👉 Bài 7. Sóng cơ và sự truyền sóng cơ
- 👉 Bài 8. Giao thoa sóng
- 👉 Bài 9. Sóng dừng
- 👉 Bài 10. Đặc trưng vật lí của âm
- 👉 Bài 11. Đặc trưng sinh lí của âm
- 👉 Đề kiểm tra 15 phút - Chương 2 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 2 – Vật lí 12
CHƯƠNG III. DÒNG ĐIỆN XOAY CHIỀU
- 👉 Bài 12. Đại cương về dòng điện xoay chiều
- 👉 Bài 13. Các mạch điện xoay chiều.
- 👉 Bài 14. Mạch có R, L, C mắc nối tiếp
- 👉 Bài 15. Công suất điện tiêu thụ của mạch điện xoay chiều. Hệ số công suất
- 👉 Bài 16. Truyền tải điện năng. Máy biến áp
- 👉 Bài 17. Máy phát điện xoay chiều
- 👉 Bài 18. Động cơ không đồng bộ ba pha
- 👉 Bài 19. Thực hành: Khảo sát đoạn mạch điện xoay chiều có R, L, C mắc nối tiếp
- 👉 Đề kiểm tra 15 phút - Chương 3 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 3 – Vật lí 12
ĐỀ THI HỌC KÌ 1 MỚI NHẤT CÓ LỜI GIẢI
CHƯƠNG IV. DAO ĐỘNG VÀ SÓNG ĐIỆN TỪ
- 👉 Bài 20. Mạch dao động
- 👉 Bài 21. Điện từ trường
- 👉 Bài 22. Sóng điện từ
- 👉 Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến
- 👉 Đề kiểm tra 15 phút - Chương 4 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 4 – Vật lí 12
CHƯƠNG V. SÓNG ÁNH SÁNG
- 👉 Bài 24. Tán sắc ánh sáng
- 👉 Bài 25. Giao thoa ánh sáng
- 👉 Bài 26. Các loại quang phổ
- 👉 Bài 27. Tia hồng ngoại và tia tử ngoại
- 👉 Bài 28. Tia X
- 👉 Bài 29. Thực hành: Đo bước sóng ánh sáng bằng phương pháp giao thoa
- 👉 Đề kiểm tra 15 phút - Chương 5 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 5 – Vật lí 12
CHƯƠNG VI. LƯỢNG TỬ ÁNH SÁNG
- 👉 Bài 30. Hiện tượng quang điện. Thuyết lượng tử ánh sáng
- 👉 Bài 31. Hiện tượng quang điện trong
- 👉 Bài 32. Hiện tượng quang - phát quang
- 👉 Bài 33. Mẫu nguyên tử Bo
- 👉 Bài 34. Sơ lược về laze
- 👉 Đề kiểm tra 15 phút - Chương 6 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 6 – Vật lí 12
CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ
- 👉 Bài 35. Tính chất và cấu tạo hạt nhân
- 👉 Bài 36. Năng lượng liên kết của hạt nhân. Phản ứng hạt nhân
- 👉 Bài 37. Phóng xạ
- 👉 Bài 38. Phản ứng phân hạch
- 👉 Bài 39. Phản ứng nhiệt hạch
- 👉 Đề kiểm tra 15 phút - Chương 7 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 7 – Vật lí 12
CHƯƠNG VIII. TỪ VI MÔ ĐẾN VĨ MÔ
- 👉 Bài 40. Các hạt sơ cấp
- 👉 Bài 41. Cấu tạo vũ trụ
- 👉 Đề kiểm tra 15 phút - Chương 8 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 8 – Vật lí 12
ĐỀ THI HỌC KÌ 2 MỚI NHẤT CÓ LỜI GIẢI
Xem Thêm
Lớp 12 | Các môn học Lớp 12 | Giải bài tập, đề kiểm tra, đề thi Lớp 12 chọn lọc
Danh sách các môn học Lớp 12 được biên soạn theo sách giáo khoa mới của bộ giáo dục đào tạo. Kèm theo lời giải sách bài tập, sách giáo khoa, đề kiểm tra 15 phút, 45 phút (1 tiết), đề thi học kì 1 và học kì 2 năm học 2024 ngắn gọn, chi tiết dễ hiểu.
Toán Học
- Đề thi, đề kiểm tra Toán lớp 12
- SBT Toán lớp 12 Nâng cao
- SBT Toán 12 Nâng cao
- SGK Toán 12 Nâng cao
- SBT Toán lớp 12
- SGK Toán lớp 12
Vật Lý
- SBT Vật lí 12 Nâng cao
- SGK Vật lí lớp 12 Nâng cao
- SBT Vật lí lớp 12
- SGK Vật lí lớp 12
- Giải môn Vật lí lớp 12
Hóa Học
- Đề thi, đề kiểm tra Hóa lớp 12
- SBT Hóa học 12 Nâng cao
- SGK Hóa học lớp 12 Nâng cao
- SBT Hóa lớp 12
- SGK Hóa lớp 12
Ngữ Văn
- Đề thi, đề kiểm tra Ngữ Văn 12 mới
- Soạn văn 12
- SBT Ngữ văn lớp 12
- Luyện dạng đọc hiểu
- Văn mẫu 12
- Soạn văn 12 chi tiết
- Soạn văn ngắn gọn lớp 12
- Soạn văn 12 siêu ngắn
- Bài soạn văn lớp 12 siêu ngắn
- Bài soạn văn 12
Lịch Sử
Địa Lý
Sinh Học
- Đề thi, đề kiểm tra Sinh lớp 12
- SGK Sinh lớp 12 Nâng cao
- SBT Sinh lớp 12
- SGK Sinh lớp 12
- Giải môn Sinh học lớp 12
GDCD
Tin Học
Tiếng Anh
- Đề thi, đề kiểm tra Tiếng Anh 12 mới
- SBT Tiếng Anh lớp 12
- Ngữ pháp Tiếng Anh
- SGK Tiếng Anh 12
- SBT Tiếng Anh lớp 12 mới
- SGK Tiếng Anh 12 Mới