Phương pháp giải một số dạng bài tập về con lắc lò xo
Lý thuyết:
Dạng 1: Tính chu kì, tần số của con lắc lò xo
Sử dụng các công thức:
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta {l_0}}}} = \frac{{2\pi }}{T} = 2\pi f\)
+ Chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \)
+ Tần số: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta {l_0}}}} \)
Với \(\Delta {l_0} = \frac{{mg}}{k}\) là độ biến dạng của lò xo khi vật ở vị trí cân bằng.
*Bài toán ghép vật
- Lò xo K gắn vật nặng m1 thì dao động với chu kì T1. Còn khi gắn vật nặng m2 thì dao động với chu kì T2. Chu kì dao động của vật khi gắn vật có khối lượng m = m1 + m2 là:
\({T^2} = T_1^2 + T_2^2\)
Tổng quát:
+ Chu kì dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:
\({T^2} = T_1^2 + T_2^2 + ... + T_n^2\)
+ Chu kì dao động của vật khi gắn vật có khối lượng m = a.m1 + b.m2 là:
\({T^2} = aT_1^2 + bT_2^2\)
- Lò xo K gắn vật nặng m1 thì dao động với chu kì f1. Còn khi gắn vật nặng m2 thì dao động với chu kì f2. Tần số dao động của vật khi gắn vật có khối lượng m = m1 + m2 là:
\(f = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }}\)
Tổng quát:
+ Tần số dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:
\(\frac{1}{{{f^2}}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} + ... + \frac{1}{{f_n^2}}\)
+ Tần số dao động của vật khi gắn vật có khối lượng m = a.m1 + b.m2 là:
\(\frac{1}{{{f^2}}} = \frac{{{a}}}{{f_1^2}} + \frac{{{b}}}{{f_2^2}}\)
Bài tập ví dụ:
Bài 1: Một con lắc lò xo nằm ngang có độ cứng k = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1 kg. Kích thích cho vật dao động điều hòa, xác định chu kì của con lắc lò xo.
Hướng dẫn giải
Ta có:
\(\left\{ \begin{array}{l}m = 0,1kg\\k = 100N/m\end{array} \right. \Rightarrow T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,1}}{{100}}} = 0,2 {\rm{s}}\)
Bài 2: Một lò xo có độ cứng là k. Khi gắn vậ m1 vào lò xo và cho dao động thì chu kì là 0,3 s. Khi gắn vật có khối lượng m2 vào lò xo trên và kích thích cho dao động thì nó dao động với chu kì là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m1 + 3m2 thì nó dao động với chu kì là bao nhiêu?
Hướng dẫn giải
Khi đó chu kì dao động của vật là:
\({T^2} = 2T_1^2 + 3T_2^2 \\\Leftrightarrow T = \sqrt {2T_1^2 + 3T_2^2} \\= \sqrt {2.0,{3^2} + 3.0,{4^2}} = 0,812s\)
Dạng 2: Chiều dài CLLX - lực đàn hồi, lực hồi phục của con lắc lò xo
1. Tính chiều dài của lò xo trong quá trình vật dao động
Gọi chiều dài tự nhiên của lò xo là l0.
- Khi con lắc lò xo nằm ngang:
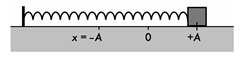
+ Lúc vật ở VTCB, lò xo không bị biến dạng,
+ Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + A\)
+ Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} - A\)
+ Chiều dài ở li độ x: \(l = {l_0} + x\)
- Khi con lắc lò xo bố trí thẳng đứng hoặc nằm nghiêng một góc αvà treo ở dưới.
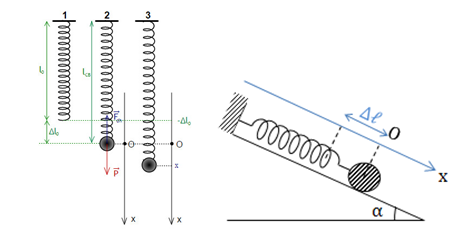
+ Độ biến dạng của lò xo khi vật ở VTCB:
- Con lắc lò xo treo thẳng đứng: \(\Delta {l_0} = \frac{{mg}}{k}\)
- Con lắc lò xo nằm nghiêng góc α: \(\Delta {l_0} = \frac{{mg\sin \alpha }}{k}\)
+ Chiều dài lò xo khi vật ở VTCB: \({l_{vtcb}} = {l_0} + \Delta l\)
+ Chiều dài ở li độ x: \(l = {l_0} + \Delta {l_0} + x\)
+ Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + \Delta {l_0} + A\)
+ Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} + \Delta {l_0} - A\)
2. Lực kéo về
\(F{\rm{ }} = - {\rm{ }}kx{\rm{ }} = - {\rm{ }}m{\omega ^2}x\)
Đặc điểm:
* Là lực gây dao động cho vật.
* Luôn hướng về VTCB
* Biến thiên điều hoà cùng tần số với li độ
3. Lực đàn hồi - Lực hồi phục cực đại, cực tiểu.Có độ lớn \({F_{dh}} = {\rm{ }}k{x^*}\) (x* là độ biến dạng của lò xo)
- Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)
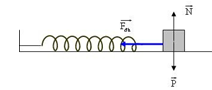
- Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng:
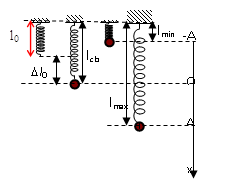
+ Độ lớn lực đàn hồi có biểu thức:
- \({F_{dh}} = {\rm{ }}k|\Delta {l_0} + {\rm{ }}x|\) với chiều dương hướng xuống
- \({F_{dh}} = k\left| {\Delta {l_0} - {\rm{ }}x} \right|\) với chiều dương hướng lên
+ Lực đàn hồi cực đại (lực kéo): \({F_{{\rm{max}}}} = k\left( {\Delta {l_0} + A} \right) = {F_{Km{\rm{ax}}}}\) (lúc vật ở vị trí thấp nhất)
+ Lực đàn hồi cực tiểu:
- Nếu\(A{\rm{ }} < \Delta {l_0} \to {F_{Min}} = {\rm{ }}k(\Delta {l_0} - {\rm{ }}A) = {F_{KMin}}\)
- Nếu \(A{\rm{ }} \ge \Delta {l_0} \to {F_{Min}} = 0\) (lúc vật đi qua vị trí lò xo không biến dạng)
+ Lực đẩy (lực nén) đàn hồi cực đại: ${F_{Nm{\rm{ax}}}} = k\left( {A - \Delta {l_0}} \right)$ (lúc vật ở vị trí cao nhất)
+ Lực đàn hồi, lực hồi phục:
- Lực đàn hồi:
\(\begin{array}{l}{F_{dh}} = k(\Delta l + x){\rm{ }}\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{d{h_{{\rm{Max}}}}}} = k(\Delta l + A){\rm{ }}}\\{{F_{d{h_{\min }}}} = k(\Delta l - A){\rm{ khi }}\Delta l > A}\\{{F_{d{h_{\min }}}} = 0{\rm{ khi}}\Delta {\rm{l}} \le {\rm{A }}}\end{array}} \right.{\rm{ }}\end{array}\)
- Lực hồi phục: \({F_{hp}} = kx{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = kA}\\{{F_{h{p_{\min }}}} = 0{\rm{ }}}\end{array}} \right.{\rm{ }}\)hay\({F_{hp}} = ma{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = m{\omega ^2}A}\\{{F_{h{p_{\min }}}} = 0{\rm{ }}}\end{array}} \right.\)
+ Lực hồi phục luôn hướng vào vị trí cân bằng.
Khi hệ dao động theo phương nằm ngang thì lực đàn hồi và lực hồi phục là như nhau ${F_{dh}} = {F_{hp}}$
Bài tập ví dụ: Một con lắc lò xo có chiều dài tự nhiên là 30 cm, độ cứng của lò xo là k = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.
Hướng dẫn giải
Độ biến dạng của lò xo khi vật ở VTCB là:
\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{10}} = 0,1m\)
Lực đàn hồi cực đại:
\({F_{\max }} = k\left( {\Delta {l_0} + A} \right) = 10.\left( {0,1 + 0,05} \right) = 1,5N\)
Lực đàn hồi cực tiểu:
\({F_{\min }} = k\left( {\Delta l - A} \right) = 10.\left( {0,1 - 0,05} \right) = 0,5N\)
Dạng 3. Bài tập năng lượng của con lắc lò xo
Phương pháp
Cho một con lắc lò xo có độ cứng k, vật có khối lượng m, dao động điều hòa với phương trình : \(x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}\) và có vận tốc: \(v = - A\omega \sin (\omega t + \varphi )\).
- Cơ năng: \(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}k{A^2}\)
- Thế năng:
\(\begin{array}{l}{W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}k{A^2}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\\ = W - {W_d} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}m{v^2}\end{array}\)
- Động năng:
\(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\)
- Đồ thị dao động:
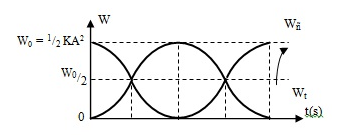
Nhận xét:
- Cơ năng được bảo toàn và tỉ lệ với bình phương biên độ.
- Vị trí thế năng cực đại thì động năng cực tiểu và ngược lại.
- Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc \(2ω\), tần số \(2f\) và chu kì \(\dfrac{T}{2}\).
- Trong 1 chu kì: có 4 lần động năng bằng thế năng. Khoảng thời gian ngắn nhất giữa hai lần động năng bằng thế năng là \(\dfrac{T}{4}\).
- Xác định vận tốc- li độ:
- Vận tốc: \({W_d} = \dfrac{1}{2}m{v^2} \to v = \pm \sqrt {\dfrac{{2{W_d}}}{m}} \)
- Li độ: \({W_t} = \dfrac{1}{2}k{x^2} \to x = \pm \sqrt {\dfrac{{2{W_t}}}{k}} \)
- Khi biết thế năng tại vị trí có li độ x gấp n lần động năng của vật: Wt = nWđ
\(\left\{ \begin{array}{l}{W_t} = n{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{n}{{n + 1}}W\\{W_d} = \dfrac{1}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm A\sqrt {\dfrac{n}{{n + 1}}} \\v = \pm \dfrac{{A\omega }}{{\sqrt {n + 1} }}\end{array} \right.\)
- Khi biết động năng tại vị trí có li độ x gấp n lần thế năng của vật: Wđ = nWt
\(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm \dfrac{A}{{\sqrt {n + 1} }}\\v = \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)
Dạng 4. Tính thời gian lò xo nén hay giãn trong một chu kì
Phương pháp:
1. Con lắc lò xo nằm ngang:
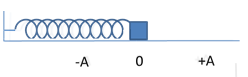
Thời gian lò xo giãn bằng thời gian lò xo nén
2. Con lắc lò xo treo thẳng đứng:
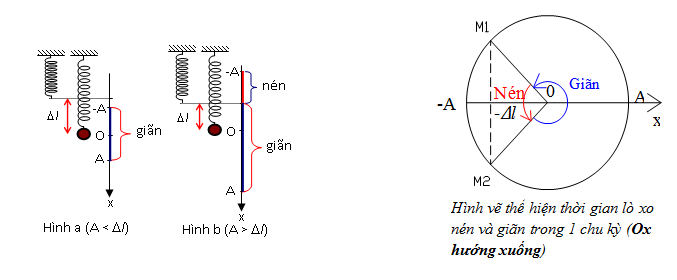
+ Khi \(A < \Delta {l_0}\) : Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
+ Khi \(A > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\) đến \({x_2} = - A\) là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\) là: \(T - \Delta t\)
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
3. Con lắc lò xo nằm nghiêng:
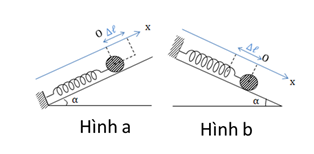
+ Khi \(A{\rm{ }} < \Delta {l_0}\) :
- Đầu cố định ở trên (Hình b): Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
- Đầu cố định ở dưới (Hình a): Trong quá trình dao động, lò xo chỉ bị nén mà không có giãn => Thời gian lò xo giãn = 0, thời gian lò xo nén = T
+ Khi \(A{\rm{ }} > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là: T-∆t
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
Dạng 5. Bài toán va chạm
1. Va chạm theo phương ngang

Vật m chuyển động với vận tốc v0 đến va chạm vào vật M đang đứng yên.
- Va chạm mềm: \(m{v_0} = (m + M)V \Rightarrow V = \frac{1}{{1 + \frac{M}{m}}}{v_0}\)
V: vận tốc của hệ hai vật M+m ở vị trí cân bằng
Nếu sau va chạm cả hai vật dao động điều hòa thì tần số và biên độ dao động của con lắc lò xo:
\(\omega = \sqrt {\frac{k}{{m + M}}} ,A = \frac{V}{\omega }\)
- Va chạm đàn hồi: \(\left\{ \begin{array}{l}m{v_0} = mv + MV\\\frac{1}{2}mv_0^2 = \frac{1}{2}m{v^2} + \frac{1}{2}M{V^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}V = \frac{2}{{1 + \frac{M}{m}}}{v_0}\\v = \frac{{1 - \frac{M}{m}}}{{1 + \frac{M}{m}}}{v_0}\end{array} \right.\)
V: vận tốc của M ở vị trí cân bằng
Nếu sau va chạm M dao động điều hòa: \(\omega = \sqrt {\frac{k}{M}} ,A = \frac{V}{\omega }\)
2. Va chạm theo phương thẳng đứng
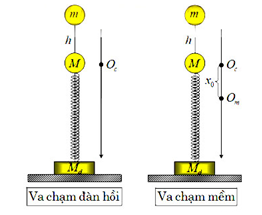
Tốc độ của m ngay trước va chạm: \({v_0} = \sqrt {2gh} \)
- Va chạm mềm:
+ Vị trí cân bằng mới thấp hơn vị trí cân bằng cũ đoạn \({x_0} = \frac{{mg}}{k}\)
+ Vận tốc của hệ sau va chạm: \(V = \frac{{m{v_0}}}{{m + M}}\)
+Biên độ sau va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí cao nhất thì sau va chạm: vật có li độ so với VTCB mới (A0+x0), biên độ mới \(A = \sqrt {{{({A_0} + {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí thấp nhất thì sau va chạm: vật có li độ so với VTCB mới (A0-x0), biên độ mới \(A = \sqrt {{{({A_0} - {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Va chạm đàn hồi:
+ \(V = \frac{{2m{v_0}}}{{m + M}} \Rightarrow A = \frac{V}{\omega },\omega = \sqrt {\frac{k}{M}} \)
+ Nếu đúng lúc vật đến vị trí biên (x=±A0) thì xảy ra va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
3. Sau va chạm đàn hồi hai vật tách rời ở vị trí cân bằng
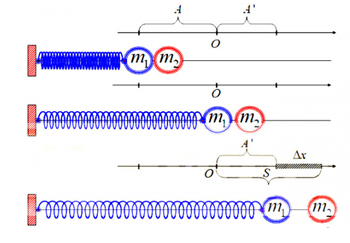
- Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc \(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} \) và tốc độ cực đại v0=ωA
- Giai đoạn 2: Nếu đến VTCB m2 tách ra khỏi m1 thì m1 dao động điều hòa với tần số góc và biên độ:
\(\omega = \sqrt {\frac{k}{{{m_1}}}} ,A' = \frac{{{v_0}}}{\omega } = A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
(Vì tốc độ cực đại không đổi vẫn là vo)
m2 chuyển động thẳng đều với vận tốc v0 và khi đến vị trí biên dương (lần 1) thì m2 đi được quãng đường: \(S = {v_0}\frac{{T'}}{4} = \frac{1}{2}\pi A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
Lúc này khoảng cách giữa hai vật: \(\Delta x = S - A'\)
Xem thêm Bài tập & Lời giải
Trong bài: Bài 2. Con lắc lò xo
Xem thêm lời giải SGK Vật lí lớp 12
CHƯƠNG I. DAO ĐỘNG CƠ
- 👉 Bài 1. Dao động điều hòa
- 👉 Bài 2. Con lắc lò xo
- 👉 Bài 3. Con lắc đơn
- 👉 Bài 4. Dao động tắt dần dao động cưỡng bức
- 👉 Bài 5. Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ FRE-NEN
- 👉 Bài 6. Thực hành: Khảo sát thực nghiệm các định luật dao động của con lắc
- 👉 Đề kiểm tra 15 phút – Chương 1 – Vật lí 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Vật lí 12
CHƯƠNG II. SÓNG CƠ VÀ SÓNG ÂM
- 👉 Bài 7. Sóng cơ và sự truyền sóng cơ
- 👉 Bài 8. Giao thoa sóng
- 👉 Bài 9. Sóng dừng
- 👉 Bài 10. Đặc trưng vật lí của âm
- 👉 Bài 11. Đặc trưng sinh lí của âm
- 👉 Đề kiểm tra 15 phút - Chương 2 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 2 – Vật lí 12
CHƯƠNG III. DÒNG ĐIỆN XOAY CHIỀU
- 👉 Bài 12. Đại cương về dòng điện xoay chiều
- 👉 Bài 13. Các mạch điện xoay chiều.
- 👉 Bài 14. Mạch có R, L, C mắc nối tiếp
- 👉 Bài 15. Công suất điện tiêu thụ của mạch điện xoay chiều. Hệ số công suất
- 👉 Bài 16. Truyền tải điện năng. Máy biến áp
- 👉 Bài 17. Máy phát điện xoay chiều
- 👉 Bài 18. Động cơ không đồng bộ ba pha
- 👉 Bài 19. Thực hành: Khảo sát đoạn mạch điện xoay chiều có R, L, C mắc nối tiếp
- 👉 Đề kiểm tra 15 phút - Chương 3 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 3 – Vật lí 12
ĐỀ THI HỌC KÌ 1 MỚI NHẤT CÓ LỜI GIẢI
CHƯƠNG IV. DAO ĐỘNG VÀ SÓNG ĐIỆN TỪ
- 👉 Bài 20. Mạch dao động
- 👉 Bài 21. Điện từ trường
- 👉 Bài 22. Sóng điện từ
- 👉 Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến
- 👉 Đề kiểm tra 15 phút - Chương 4 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 4 – Vật lí 12
CHƯƠNG V. SÓNG ÁNH SÁNG
- 👉 Bài 24. Tán sắc ánh sáng
- 👉 Bài 25. Giao thoa ánh sáng
- 👉 Bài 26. Các loại quang phổ
- 👉 Bài 27. Tia hồng ngoại và tia tử ngoại
- 👉 Bài 28. Tia X
- 👉 Bài 29. Thực hành: Đo bước sóng ánh sáng bằng phương pháp giao thoa
- 👉 Đề kiểm tra 15 phút - Chương 5 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 5 – Vật lí 12
CHƯƠNG VI. LƯỢNG TỬ ÁNH SÁNG
- 👉 Bài 30. Hiện tượng quang điện. Thuyết lượng tử ánh sáng
- 👉 Bài 31. Hiện tượng quang điện trong
- 👉 Bài 32. Hiện tượng quang - phát quang
- 👉 Bài 33. Mẫu nguyên tử Bo
- 👉 Bài 34. Sơ lược về laze
- 👉 Đề kiểm tra 15 phút - Chương 6 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 6 – Vật lí 12
CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ
- 👉 Bài 35. Tính chất và cấu tạo hạt nhân
- 👉 Bài 36. Năng lượng liên kết của hạt nhân. Phản ứng hạt nhân
- 👉 Bài 37. Phóng xạ
- 👉 Bài 38. Phản ứng phân hạch
- 👉 Bài 39. Phản ứng nhiệt hạch
- 👉 Đề kiểm tra 15 phút - Chương 7 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 7 – Vật lí 12
CHƯƠNG VIII. TỪ VI MÔ ĐẾN VĨ MÔ
- 👉 Bài 40. Các hạt sơ cấp
- 👉 Bài 41. Cấu tạo vũ trụ
- 👉 Đề kiểm tra 15 phút - Chương 8 - Vật lý 12
- 👉 Đề kiểm tra 45 phút (1 tiết) – Chương 8 – Vật lí 12
ĐỀ THI HỌC KÌ 2 MỚI NHẤT CÓ LỜI GIẢI
Xem Thêm
Lớp 12 | Các môn học Lớp 12 | Giải bài tập, đề kiểm tra, đề thi Lớp 12 chọn lọc
Danh sách các môn học Lớp 12 được biên soạn theo sách giáo khoa mới của bộ giáo dục đào tạo. Kèm theo lời giải sách bài tập, sách giáo khoa, đề kiểm tra 15 phút, 45 phút (1 tiết), đề thi học kì 1 và học kì 2 năm học 2024 ngắn gọn, chi tiết dễ hiểu.
Toán Học
- Đề thi, đề kiểm tra Toán lớp 12
- SBT Toán lớp 12 Nâng cao
- SBT Toán 12 Nâng cao
- SGK Toán 12 Nâng cao
- SBT Toán lớp 12
- SGK Toán lớp 12
Vật Lý
- SBT Vật lí 12 Nâng cao
- SGK Vật lí lớp 12 Nâng cao
- SBT Vật lí lớp 12
- SGK Vật lí lớp 12
- Giải môn Vật lí lớp 12
Hóa Học
- Đề thi, đề kiểm tra Hóa lớp 12
- SBT Hóa học 12 Nâng cao
- SGK Hóa học lớp 12 Nâng cao
- SBT Hóa lớp 12
- SGK Hóa lớp 12
Ngữ Văn
- Đề thi, đề kiểm tra Ngữ Văn 12 mới
- Soạn văn 12
- SBT Ngữ văn lớp 12
- Luyện dạng đọc hiểu
- Văn mẫu 12
- Soạn văn 12 chi tiết
- Soạn văn ngắn gọn lớp 12
- Soạn văn 12 siêu ngắn
- Bài soạn văn lớp 12 siêu ngắn
- Bài soạn văn 12
Lịch Sử
Địa Lý
Sinh Học
- Đề thi, đề kiểm tra Sinh lớp 12
- SGK Sinh lớp 12 Nâng cao
- SBT Sinh lớp 12
- SGK Sinh lớp 12
- Giải môn Sinh học lớp 12
GDCD
Tin Học
Tiếng Anh
- Đề thi, đề kiểm tra Tiếng Anh 12 mới
- SBT Tiếng Anh lớp 12
- Ngữ pháp Tiếng Anh
- SGK Tiếng Anh 12
- SBT Tiếng Anh lớp 12 mới
- SGK Tiếng Anh 12 Mới