Câu 76 trang 65 Sách bài tập Hình học 11 nâng cao.

Đề bài

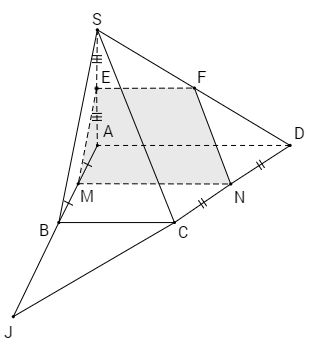
Cho hình chóp S.ABCD có đáy là hình thang \(\left( {AD//BC,\,AD > BC} \right).\) Gọi M, N, E lần lượt là trung điểm của AB, CD, SA.

a) Chứng minh rằng:

\(MN//\left( {SBC} \right);\,\left( {MEN} \right)//\left( {SBC} \right).\)

b) Trong tam giác SAD vẽ EF//AD \(\left( {F \in SD} \right).\) Chứng minh rằng F là giao điểm của mặt phẳng (MNE) với SD. Từ đó suy ra thiết diện của hình chóp khi cắt bởi mp(MNE) là hình gì?

c) Chứng minh rằng SC//(MNE). Đường thẳng AF có song song với mp(SBC) hay không?

d) Cho M, N là hai điểm cố định lần lượt nằm trên các cạnh AB, CD sao cho MN//AD và E, F là hai điểm di động lần lượt trên các cạnh SA, SD sao cho EF//AD. Gọi I là giao điểm của ME và NF thì I di động trên đường nào?

Lời giải chi tiết

a) MN là đường trung bình của hình thang ABCD, suy ra:

\(\eqalign{
& \left. \matrix{
MN//BC \hfill \cr 
BC \subset \left( {SBC} \right) \hfill \cr} \right\} \Rightarrow MN//\left( {SBC} \right) \cr 
& \left. \matrix{
MN//\left( {SBC} \right) \hfill \cr 
ME//\left( {SBC} \right) \hfill \cr} \right\} \Rightarrow \left( {MEN} \right)//\left( {SBC} \right) \cr} \)

b) Ta có 

\(\eqalign{
& EF//AD \Rightarrow EF//MN \cr 
& \Rightarrow EF \subset \left( {MNE} \right) \Rightarrow F \in \left( {MNE} \right). \cr} \)

Mặt khác \(F \in SD,\) do đó \(F = \left( {MNE} \right) \cap SD.\)

Thiết diện là hình thang MNFE.

c) Theo câu a), ta có \(\left( {SBC} \right)//\left( {MNE} \right)\) mặt khác \(SC \subset \left( {SBC} \right)\)

Suy ra              SC // (MNE).

Đường thẳng AF không song song với mp(SBC) vì nếu AF // (SBC) thì :

\(AF \subset \left( {MNE} \right) \Rightarrow A \in \left( {MNE} \right)\) (vô lí).

d) Xét ba mặt phẳng (SAB), (SCD) và (MNE). Ta có:

\(\left( {SAB} \right) \cap \left( {SCD} \right) = SJ\) (J là giao điểm của AB và CD)

\(\eqalign{
& \left( {SAB} \right) \cap \left( {MNE} \right) = ME \cr 
& \left( {SCD} \right) \cap \left( {MNE} \right) = NF \cr} \)

Theo định lí về giao tuyến của ba mặt phẳng thì ba đường thẳng SJ, ME, NF đồng quy. Vậy điểm I phải di động trên đường thẳng SJ (trừ những điểm trong của đoạn SJ).

Xemloigiai.com